문제 요약
길이 N일 배열이 주어진다. 쿼리로는 [l,r,k]가 주어지는데 이는 배열 a[i...j]에서 k번째 수를 출력하라는 뜻이다.
N은 최대 10만이고 쿼리 수는 최대 5000이다.
풀이
먼저 좌표압축을 하자. 좌표압축을 한 좌표들의 길이로 구간 합 세그먼트 트리를 만들도록 하자.
a[1]부터 시작해서 a[N]까지 돌면서 a[i]에 해당하는 위치의 원소를 1씩 늘려줍니다. 이 때, 해당 세그먼트 트리를 PST로 만들어서 i번째 원소를 추가했을 때의 세그먼트 트리에 접근이 가능하도록 합시다.
a가 [1,5,2,6,3,7,4]라고 하면 아래와 같이 업데이트가 진행되고 색깔이 바뀌는 부분들만 새롭게 노드를 추가하면 됩니다.






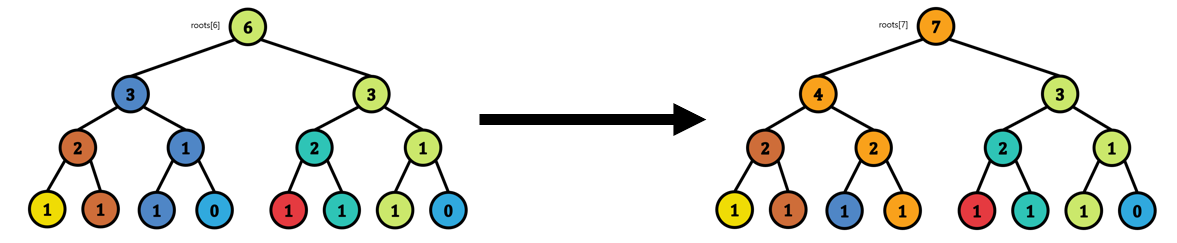
이런식으로 세그먼트트리가 갱신된다고 합시다.
i번째 원소를 업데이트한 세그먼트 트리의 루트 노드를 roots[i]라고 합시다. 그러면 이 세그먼트 트리는 1...i번까지의 원소들의 정보를 들고 있다고 할 수 있습니다.
그러면 이제 roots[r]에 해당하는 세그먼트 트리에서 roots[l-1]에 해당하는 세그먼트 트리의 원소들을 빼주면 이제 [l, r]에 속하는 원소들의 정보를 갖고 있는 세그먼트 트리를 가질 수 있습니다.
해당 세그먼트 트리는 좌표압축한 결과에 대해서 만들었으므로 해당 세그먼트 트리에서 K번째 원소를 찾아주면 [l.r]에서의 K번째 원소를 찾는 것과 동일합니다.
이걸로 쿼리를 $O(logN)$에 해결이 가능합니다.
세그먼트 트리에서 K번째 원소를 찾는 것은 노드를 타고 내려갈 때 왼쪽 자식노드의 합이 K보다 작으면 오른쪽으로 내려가면서 그만큼 K에서 빼주고 크거나 같으면 왼쪽으로 내려가는 식으로 진행하면 됩니다.
#include<bits/stdc++.h>
using namespace std;
struct Node {
int l, r, val;
};
int N, Q;
int a[100005], roots[100005];
int node_cnt;
vector<int> comp;
vector<Node> tree(100000 * 30);
void init_tree() {
node_cnt = comp.size() << 1;
for (int i = 1; i < comp.size(); ++i) {
tree[i].l = i << 1;
tree[i].r = i << 1 | 1;
}
}
void update(int node, int s, int e, int val, int idx) {
tree[node].val += val;
if (s != e) {
int mid = s + e >> 1;
int n1 = tree[node].l, n2 = tree[node].r;
if (idx <= mid) {
tree[node].l = node_cnt;
tree[node_cnt++] = tree[n1];
update(tree[node].l, s, mid, val, idx);
}
else {
tree[node].r = node_cnt;
tree[node_cnt++] = tree[n2];
update(tree[node].r, mid + 1, e, val, idx);
}
}
}
int get_kth(int nxt_node, int prv_node, int s, int e, int k) {
if (s == e) return s;
int lsz = tree[tree[nxt_node].l].val - tree[tree[prv_node].l].val;
int mid = s + e >> 1;
if (lsz >= k) return get_kth(tree[nxt_node].l, tree[prv_node].l, s, mid, k);
else return get_kth(tree[nxt_node].r, tree[prv_node].r, mid + 1, e, k - lsz);
}
int main() {
cin.tie(nullptr); ios::sync_with_stdio(false);
cin >> N >> Q;
for (int i = 1; i <= N; ++i) {
cin >> a[i];
comp.push_back(a[i]);
}
sort(comp.begin(), comp.end());
comp.erase(unique(comp.begin(), comp.end()), comp.end());
for (int i = 1; i <= N; ++i) a[i] = lower_bound(comp.begin(), comp.end(), a[i]) - comp.begin();
init_tree();
roots[0] = 1;
for (int i = 1; i <= N; ++i) {
roots[i] = node_cnt++;
tree[roots[i]] = tree[roots[i - 1]];
update(roots[i], 0, comp.size() - 1, 1, a[i]);
}
for (int i = 0; i < Q; ++i) {
int l, r, k; cin >> l >> r >> k;
int idx = get_kth(roots[r], roots[l - 1], 0, comp.size() - 1, k);
cout << comp[idx] << '\n';
}
return 0;
}'Problem Solving > 문제풀이' 카테고리의 다른 글
| 백준 13538번 XOR 쿼리 (0) | 2021.02.16 |
|---|---|
| 백준 11012번 Egg (0) | 2021.02.16 |
| 백준 14176번 트리와 소수 (0) | 2021.02.16 |
| 백준 13431번 트리 문제 (0) | 2021.02.16 |
| 백준 5820번 경주 (0) | 2021.02.16 |