Introduction
디퓨전 계열이 생성 모델에서 엄청난 성능을 보여주며 주류가 되어 버린지는 한참 되었다. 그러나 여러 번에 걸친 샘플링이 디퓨전 모델의 좋은 성능을 만들어 주는 것처럼 보이지만 이는 동시에 추론 속도가 느려진다는 뜻이다.
그래서 디퓨전 모델보다 더 빠르고, 더 좋은 모델을 만들어 보려는 연구는 꾸준히 존재했고 Flow Matching은 그런 연구 중 하나다. Flow Matching을 제안하는 논문은 동 시기에 여러개가 등장했으며 Flow Matching for Generative Modeling 논문은 그 중의 하나이다. 추가로, 최근 Stable Diffusion3가 Flow Matching 기반의 모델이라고 해서 좀 더 관심을 한번 더 모으고 있는 것 같다.
이 글은 Flow Matching for Generative Modeling 논문을 토대로 Flow Matching을 정리한 글이다.
Continuous Normalizing Flows
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs based on regressing vector fields of fixed conditional probability paths.
위는 논문의 초록 중 일부로, 초록에서 밝히듯이 Flow Matching은 Continuous Normalizing Flow (CNF)를 시뮬레이션 없이 효율적으로 훈련하는 방법이다. 먼저, CNF가 무엇인지 알아야 좀 더 얘기를 이해하기 쉬워진다.
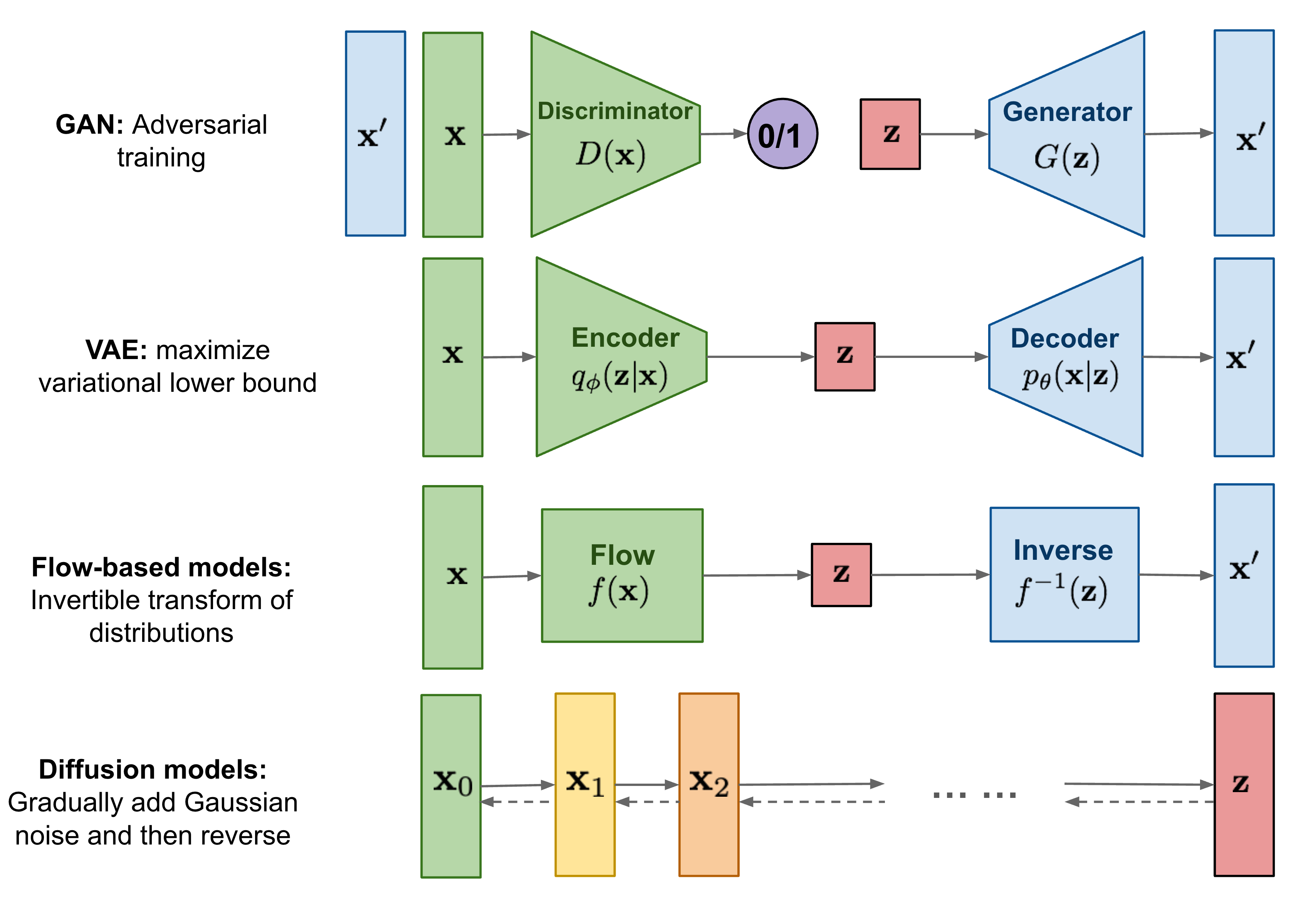
위 그림과 같이 대부분의 생성 모델은 우리가 잘 알고 샘플링하기 쉬운 분포 $z$에서 생성하기 원하는 분포 $x$로의 변환을 학습하게 된다. 많은 경우 $z$는 가우시안이고, $x$는 데이터가 된다.
Normalizing Flow는 데이터 분포인 $x$에서 $z$로의 역변환이 가능한 flow를 뉴럴 네트워크 $f$가 학습하는 것이 목적이다. 뉴럴 네트워크 $f$는 역변환이 가능하기 때문에 생성 시에는 $z$에서 뽑은 샘플 $z_0$에 $f^{-1}$을 적용하게 되면 데이터 생성이 가능해진다.
CNF는 Neural Ordinary Differential Equations[^4]에서 제시됐는데 뉴럴 넷 $f$가 변환 자체인 flow를 학습하는 것이 아니라, flow의 vector field를 학습하도록 정의한다.
$$
\frac{d}{dt}x_t = f(x_t, t)
$$
뉴럴 넷이 vector field를 타겟으로 학습하도록 세팅을 하면 기존 Normalizing Flow의 제약사항이었던 $f$에 역변환이 있어야 한다는 제약이 없어진다. $f$가 $t \in [0, 1]$에서 정의되고 $t=0$일 때 시작 분포를 $z$, $t=1$일 때의 분포를 데이터 분포로 놓게 되면 $z$에서 샘플링을 통해 얻은 $x_0$에 대해서 아래와 같은 식을 계산해주면 생성이 가능해지게 된다.
$$
x_0 + \int_0^1{f(x, t)}dt
$$
적분은 ODE Solver를 통해서 계산을 수행하게 된다. 다만, $z$와 $x$에서 얻은 데이터만 가지고 있기 때문에, 학습 또한 source distribution $z$에서 샘플을 얻은 뒤 ODE Solver를 사용하여 적분을 수행하여 진행된다. 실제로 학습은 Maximum Likelihood Estimation을 통해 이루어지며 자세한 내용은 Neural Ordinary Differential Equation 논문에 있다.
Flow Matching
CNF는 굉장히 강력한 프레임워크이지만 많은 데이터셋에 대해서 학습하기가 굉장히 어렵다. 학습 과정 중에 적분을 수행해야 하기 때문에 ODE Solver를 통해서 여러번의 forward가 필요하기 때문이다. 간단하게 말해서, Diffusion 모델의 느린 샘플링 과정을 매 학습마다 수행해야 하는 것이다.
이제 글의 목표인 Flow Matching이 어떻게 simulation-free, 즉 실제 적분 과정 없이 CNF를 학습 가능하게 하는지 알아보자.
Notation
시간 $t \in [0, 1]$: $t=1$일 때가 data이며, $t=0$일 때가 source distribution이다.
$u_t, v_t$: $t$ 시점의 vector field, $u_t$는 학습 중에 타겟으로 잡는 것이며 $v_t$는 학습한 vector field이다.
$x_t$: $x_0$부터 시작해서 $u_t$를 따라 $t$까지 적분한 값
$p_t$: $x_t$의 pdf. $p_0(x)$를 알고 있고, vector field를 알고 있다면 $p_t(x)$ 또한 계산이 가능. $p_t(x)$를 줄여 쓴 것.
Flow Matching Loss
Flow Matching은 MLE를 통해서 학습을 수행하는 것이 아니라 CNF의 vector field에 대한 regression을 통해 학습을 수행한다.
문제 세팅부터 다시 해보자. $x_1$은 우리가 알지 못하는 데이터의 분포 $q(x_1)$에서 얻은 샘플들로, 생성 모델을 훈련하고자 하는 데이터셋이다. probability density path $p_t$를 정의할 것인데, $p_t$는 우리가 알고 있는 쉬운 분포 $p$가 $p_0$이고, $p_1=q$가 되도록 하고 싶다.
그리고, $u_t$가 $p_t$를 생성하도록 하는 vector field라고 하면 Flow Matching Loss를 아래와 같이 정의한다.
$$
\mathcal{L}_{FM}(\theta) = \mathbb{E}_{t, p_t(x)}\Vert u_t(x) - v_t(x) \Vert
$$
여기서 $v(x_t)$는 앞서 정리했듯이, 뉴럴 넷이 학습한 vector field이다. 이 로스값이 0이 된다면 우리는 $p_0$에서부터 $p_t$를 만들 수 있게 된다.
하지만, $p_t(x)$, 그리고 vector field인 $u_t(x)$를 모른다. 여기서 Flow Matching은 probability path에 대한 supervision을 사용하여 로스를 사용할 수 있게 한다. 우리가 직접 $p_t$와 $u_t$를 만들어주는 것이다.
당연히 전체 분포에 대한 것을 임의로 만들 수는 없고 샘플 별로 $p_t$와 $u_t$를 디자인해준다. 이제 어떻게 이를 디자인하고 샘플 별로 만들어준 $p_t(x | x_1)$, $u_t(x|x_1)$이 어떻게 전체 분포에 대한 expectation이 될 수 있는지 알아보자.
Conditional Flow Matching
이제 샘플 별로 conditional probability path, $p_t(x|x_1)$를 정의하도록 하자. 그리고 이러한 probability path를 만들어내는 vector field를 $u_t(x|x_1)$라고 하자.
그렇게 놓고 Conditional Flow Matching Loss를 아래 식으로 정의하자.
$$
\mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t, q(x_1), p_t(x|x_1)} \Vert u_t(x|x_1) - v_t(x) \Vert
$$
이렇게 샘플 별로 로스를 정의한 다음 최적화를 진행하여도 문제는 없을까?
Flow Matching for Generative Modeling 논문의 Theorem 1과 Theorem 2가 $\mathcal{L}_{CFM}$에 대하여 최적화를 수행해도 문제가 없음을 증명한다. 각 정리에 대해서 간단하게 설명하기 위해 먼저 marginal probability path $p_t(x)$와 $u_t(x)$에 대해서 정의하자.
$$
p_t(x) = \int{p_t(x|x_1)q(x_1)dx_1}
$$
$$
u_t(x) = \int{u_t(x|x_1)\frac{p_t(x|x_1)q(x_1)}{p_t(x)}dx_1}
$$
Theorem 1은 conditional probability path $p_t(x|x_1)$을 만드는 conditional vector field $u_t(x|x_1)$가 있다면, 위에서 정의한 $u_t(x)$가 실제로 $p_t(x)$를 만든다는 정리이다.
Theorem 2은 간단한데, $\nabla_\theta{\mathcal{L}_{FM}}=\nabla_\theta{\mathcal{L}_{CFM}}$라는 정리이다. 즉, sample 별로 최적화를 수행하고 expectation을 구하는 식으로 최적화를 진행해도 된다는 뜻이다.
각 정리에 대한 증명은 논문의 Appendix에 있다.
이걸로 적당한 supervision을 통해 ode solver 필요 없이 CNF를 학습하는 방법을 알았다. 이제 필요한 것은 적절하게 $p_t, u_t$를 정하는 것이다.
Gaussian Path
샘플 별로 conditional probability path $p_t(x|x_1)$와 conditional vector field $u_t(x|x_1)$를 정의해서 학습을 수행하면 된다.
충분히 강하면서도 간단한 방법은 논문에서도 설명하고 있는 아래와 같은 Gaussian Path $p_t$이다.
$$
p_t(x_t|x_1) = \mathcal{N}(\mu_t(x_1), \sigma_t^2(x_1)I)
$$
여기서 $\mu_t, \sigma_t$에 대한 조건을 아래와 같이 사용한다.
$$
\begin{aligned}
\mu_0(x_1) = 0, & \; \sigma_0(x_1) = 1 \\
\mu_1(x_1)=x_1, & \; \sigma_1(x_1) = \sigma_\min
\end{aligned}
$$
$\sigma_\min$을 충분히 작은 값으로 정의하게 되면, 이 조건은 $p_1(x_1) = \mathcal{N}(x_1, \sigma_\min^2I)$, $p_0(x_1)=\mathcal{N}(0, I)$로 source distribution을 정규 가우시안으로 놓고 $t=1$일 때는 data point에 모여 있는 가우시안이 된다.
이렇게 정의해주고 나면 $x_t = \sigma_t(x_1)x_0 + \mu_t(x_1)$이며, $u_t(x_t|x_1)$는 아래와 같이 식이 유도된다.
$$
u_t(x_t|x_1) = \frac{\sigma_t'(x_1)}{\sigma_t(x_1)}(x_t - \mu_t(x_1)) + \mu_t'(x_1)
$$
이를 통해서 Gaussian Path를 사용하는 Flow Matching 학습이 가능해진다. 위에서 정한 조건은 $t=0,1$일 때의 boundary condition이고 이를 만족하는 gaussian path라면 학습이 가능하다.
Optimal Transport
논문에서는 gaussian path $p_t$의 예시로 Diffusion과 Optimal Transport를 사용했으며, Diffusion이 Flow Matching에 포함될 수 있음을 보여줬다. 이 글에서는 optimal transport만을 간략하게 소개하고 넘어가려고 한다.
Optimal Transport란, noise에서 data sample까지 직선으로 가는 path이다. 아래와 같이 $t=0$에서 $t=1$로 갈 때 $t=0$에서는 noise, $t=1$일 때는 데이터 포인트 주변의 분포이며 그 사이에서는 직선으로 정의된다.
$$
\begin{aligned}
\mu_t(x_1) &= tx_1, \text{ and } \sigma_t(x_1) = 1 - (1 - \sigma_\min)t \\
x_t &= (1 - (1 - \sigma_\min)t)x_0 + tx_1 \\
u_t(x_t | x_1) &= x_1 - (1 - \sigma_\min)x_0
\end{aligned}
$$
위 식들을 $\mathcal{L}_{CFM}$에 넣어주면 학습이 가능하다.
Implementation
실제 cifar 10에 대해서 구현해둔 예제 노트북 링크이다.
실질적으로 학습하는 부분만 가져와본다면 아래와 같다.
for samples in dataloader:
x1 = samples["pixel_values"] # data
t = torch.rand((x.shape[0], )).to(x1) # timestep sampling
t = t.view(-1, 1, 1, 1)
x0 = torch.randn_like(x) # sample from gaussian, p0
xt = (1 - (1 - sigma) * t) * x0 + t * x1 # optimal transport를 사용한 x_t 계산
flow = x - (1 - sigma) * x0 # target이 되는 vector field
t = t.squeeze()
vt = model(xt, t) # vector field 추론
loss = F.mse_loss(flow, vt) # vector field와 regression 로스 계산
optimizer.zero_grad()
loss.backward()
optimizer.step() # update$p_0=\mathcal{N}(0, I)$에서 샘플링한 $x_0$를 얻은 다음 데이터 $x_1$과 optimal transport를 통해 정의한 $x_t$와 $u_t(x_t|x_1)$을 계산한다.
그 뒤, 뉴럴 넷에 $x_t$와 $t$를 넣어 $v_t(x_t|x_1)$를 얻은 다음 $u_t(x_t|x_1)$와 $v_t(x_t|x_1)$간의 mse loss를 사용하여 학습을 진행한다.
추론을 수행할 때는 아래처럼 noise를 샘플링한 뒤에 ode solver를 사용하면 생성이 가능해진다.
# Euler
with torch.no_grad():
x = torch.randn((batch_size, 3, 32, 32)).cuda()
times = torch.linspace(0, 1, n_steps).cuda()
dt = 1 / n_steps
for t in tqdm(times):
v = model(x, t.repeat(batch_size))
x = x + dt * v정리
Flow Matching에 대해서 다뤄보았다. 아마 디퓨전을 이미 잘 알고 계신 분들이라면 v-prediction하고 같지 않나? 스케쥴러만 잘 조절해주면 디퓨전도 optimal transport처럼 되지 않나? 라고 생각할 사람이 있을 것 같다.
글에서 다룬 논문에서는 Gaussian Path만을 다뤘지만 실제로는 Flow Matching에서 gaussian path여야만 한다는 제약 조건은 없다. 그렇기 때문에 Flow Matching을 Diffusion의 슈퍼 셋으로 바라보면 좋을 것 같다.
추가로, 논문의 저자가 직접 설명해주는 동영상이 있으니 관심이 더 생겼다면 아래 동영상을 봐도 좋을 것 같다.
https://youtu.be/5ZSwYogAxYg?si=hlkCEuJLS976o8yt
References
1: Lipman, Y., Chen, R. T. Q., Ben-Hamu, H., Nickel, M., and Le, M. Flow matching for generative modeling. In The Eleventh International Conference on Learning Representations, 2023
2: Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David K Duvenaud. Neural ordinary differential equations. Advances in neural information processing systems, 31, 2018.
'Machine Learning' 카테고리의 다른 글
| so-vits-svc 구조 정리 (2) | 2023.07.01 |
|---|---|
| 연구프로젝트 샘플 (0) | 2021.12.24 |
| Transfer Learning from Speaker Verfication to Multispeaker Text-To-Speech Synthesis 리뷰 (0) | 2021.10.07 |
| 딥러닝을 활용한 음성합성(TTS) 훑어보기(Vocoder) (0) | 2021.09.11 |
| 딥러닝을 이용한 음성합성(TTS) 훑어보기(Text-to-Mel) (0) | 2021.09.08 |


