유튜브에 있는 MIT의 6.006 수업의 해시부분을 보고 정리한 내용입니다.
Dictinoary ADT
사전(Dictionary)라고 부르는 자료구조가 있다. 파이썬의 Dictionary가 이 기능을 하는 자료구조이다. 기능은 간단하다.
key와 item이 있을 때 이 사전에 key에 대응하는 item을 삽입하고(Insert), key에 대응하는 item이 현재 사전에 있는지 확인하고(Search), 특정 key에 해당하는 item을 삭제할 수 있어야 한다.(Delete)
이를 구현하기 위해서 생각할 수 있는 방법은 두 가지가 있겠다.
key 끼리의 비교연산을 기반으로 balanced tree(Red-black Tree, Splay Tree, B+-tree)등을 이용해서 구현하는 것이다. 이런 자료구조를 기반으로 만들었을 때 각 연산의 시간복잡도는 $O(\log N)$임이 증명되어 있다. 이 시간복잡도도 나쁘진 않지만 더 빨랐으면 좋겠다. DB나 대형 라우터라면 이걸론 좀 느릴 수 있다.
트리를 사용하지 않고 사전을 구현하는 또 다른 방법은 해시 테이블을 사용하는 것이다.
Simplest Method
사전을 구현하기 위한 가장 간단한 방법은 그냥 엄청 엄청 큰 배열을 만들어서 key를 인덱스로 사용하여 저장하는 것이다.
그런데 이걸 왜 못할까?
첫 째로 key가 꼭 정수라는 보장이 없다. 파이썬의 사전을 생각해보자. Hashable이란 특성을 만족하는 다양한 자료형이 key로 사용가능하다.
table = dict()
table[1] = "Integer"
table["string_key"] = "String"
table[1.5] = "Floating Number"
table[(1, 1)] = "tuple"정수가 아니면 배열의 인덱스로 사용할 수 없다.
둘 째로 배열로 사용해야 되는 메모리가 너무 크다. key로 32비트 정수형을 쓴다고 해보자. 크기가 40억인 배열을 만들어둬야 한다. 64비트라면? 다른 방법을 찾는게 정신건강에 이롭다.
이 두 문제를 해결해보자.
Prehash
컴퓨터는 0하고 1만 알아듣는다는 소리를 들어봤을거다. 어떤 key가 들어오든 그 키는 메모리 상에서 결국 비트열로 표현된다. 그리고 비트열은 정수다.
사실 꼭 정수라는 보장이 없다는 문제는 컴퓨터 상에서 문제가 아니었던 것이다. 하지만 이건 어디까지나 이론 상의 얘기다.
ASCII로 이루어진 문자열의 길이가 10이었다면 비트로는 80비트고 이를 직접 쓰기엔 상당히 크다.
그래서 key들을 적당히 작은 범위(32-bit 정수, 64-bit 정수)로 매핑 시켜줄 필요가 있다. 이런 과정을 prehash라고 한다.
파이썬에서는 hash라는 함수가 있는데 이 함수가 하는 역할이 prehash라고 생각하면 된다.

prehash를 해주는 함수를 라고 해보자. 당연히 이상적인 상황이라면 두 key 가 다르다면 도 달라야 할 것이다. 하지만 실제로 그렇게 하는 것은 꽤 힘들다. 아래는 서로 다른 key에 대해 Python2의 hash가 서로 같은 해시 값을 같는 경우다.

이런식으로 적당히 작은 정수로 매핑시켜주는 함수 중 유명한 것으로는 MurMurHash나 페이스북의 XXHash가 있다. 이 함수들은 여러 공격에 있어서 안전하지 않은 대신에 빠르고 충돌 확률이 적다. SHA-256 같은 것은 공격에 있어서 안전하게 설계됐지만 느리다.
현재는 XXHash3가 상당히 빠르다고 한다. 물론 key의 크기에 따라서 성능이 달라지는 면이 있기 때문에 자기 프로젝트에 넣고 해시 테이블을 넣고 싶다면 실험해보고 넣는게 좋다. 혹은 언어가 제공하는 해시 테이블이 있다면 그걸 쓰는 것도 좋은 선택이다.
이걸로 첫 번째 문제인 key들이 정수가 아닐수도 있는 점은 해결됐다.
하지만 엄청난 메모리가 필요하다는 두번째 문제는 그대로다.
Hashing
이제 해싱이 등장할 차례다. 사람들이 굳이 prehash와 hash를 구분해서 부르지 않는 이유는 위 prehash 과정과 이 hashing 과정을 합쳐서 해시라고 불러서인거 같다.
해싱이 하는 일 또한 prehash와 같다. 다만 우리 메모리에 올릴만큼의 크기의 공간으로 key들을 매핑시켜주는 것이다.
실제 item을 저장할 배열의 크기를 $m$이라고 하자. 그러면 해시함수 $h$는 key를 배열의 인덱스인 $[0, m-1]$에 존재하는 정수로 매핑시켜주는 역할을 한다.
이 때 각 인덱스에 해당하는 곳은 bucket이라고도 부른다.
그게 다다. 이걸로 두 번째 문제도 해결됐다.
하지만 prehash든 hash든 저 매핑을 잘 디자인해야된다는 새로운 문제가 생겼다. 지금부턴 위에서 언급한 해시함수 $h : Z \rightarrow Z_m$에 집중해보자.
Collision
충돌(Collision)은 해시 테이블에서 중요한 문제다. 충돌이 어떤 것인지부터 알아보자.
해시 테이블의 크기가 $M$이라고 해보자. 저장해야 되는 key의 개수 $N$이 $M$보다 크다면 비둘기집의 원리에 의해서 적어도 두 개의 key는 같은 bucket으로 매핑이 된다.
이런 식으로 서로 다른 키 $x, y$의 해시값인 $h(x), h(y)$가 같아서 해시 테이블에서 같은 bucket으로 매핑되는 것을 충돌이라고 부른다.
해시함수를 정말 기막히게 정의해서 모든 bucket에 매핑될 확률이 균등하다고 해보자. 그럼에도 이러한 충돌을 상당히 자주 일어나고 따라서 이를 잘 처리하는 것이 해시 테이블의 주요 과제이다. (Birthday Paradox를 찾아보면 좋다)
서로 다른 키가 테이블에서 같은 곳을 가리키면 덮어 씌울 수는 없으니까 이를 적절히 해결해야 한다.
충돌에 대응하는 방법으로 대표적인 것은 Open Addressing이라고 부르는 것과 Chaining이 있다.
Open Addressing
Open Addressing은 Probing이라는 방식을 이용해서 충돌을 해결한다. Probing이라는 것은 충돌이 발생했을 때 그 자리를 이미 가지고 있는 key를 놔두고 새로운 자리를 찾는 과정이다.
또, Open Addressing 방식은 해시 테이블의 크기가 삽입, 삭제 도중에 변하지 않는다. 이런 방식을 static hashing scheme이라고 하는 거 같다.
해시 함수 $h$를 생각해보자. 이 함수는 key를 $[0,.., m-1]$사이의 인덱스로 매핑시켜주는 함수였다. 이 함수에다가 trial이라는 인자를 하나 더 추가하는 것이다.
trial은 현재 충돌이 일어난 횟수라고 생각하면 된다. 어떤 key $x$를 삽입한다고 생각해보자. 그러면 제일 처음엔 $h(x, 0)$을 통해서 bucket을 계산한다.
충돌이 발생했다면 $h(x, 1)$을 통해서 다음 bucket을 계산한다.
이런 함수에서 중요한 점은 특정 key $x$에 대해서 $h(x,0), h(x, 1), ... , h(x, m-1)$이 0부터 m-1까지의 수를 하나씩 갖는 permutation이어야 좋다는 점이다. 이런 permutation이 아니라면 key의 분배가 잘 이루어지지 않을 것이다.
이런 해시 방식의 일종으로 Linear Probing, Double Hashing 등이 있다.
Linear Probing은 key만을 인자로 받는 해시 함수 $h'$가 있고 $h(x,i)= h'(x)+i \pmod m$로 사용하는 것이다.
Double Hashing이라는 것은 해시 함수 $h_1, h_2$ 두 개를 사용하는 것이다. $h(x, i)=h_1(x)+ih_2(x) \pmod m$일 때 $h_2(x)$와 $m$이 서로소라면 $h(x, i)$는 0부터 m-1까지의 수를 하나씩 갖는 permutation이 된다.
여기선 Linear Probing을 사용해서 해시테이블의 삽입, 삭제, 검색이 어떻게 이뤄지는지 알아보자.
Probing을 이용한 해시 테이블에서 삽입은 빈 bucket이 있을 때까지 계속해서 해시를 시도해본 다음에 빈 슬롯을 발견하면 그 자리에 key/item을 삽입한다. 아래 그림에서 A라는 key가 삽입되어 있고 B를 삽입하려고 한다. B는 0에 매핑이 됐고 비어 있기 때문에 끝이다.
C를 삽입하려고 하지만 처음에 매핑된 곳은 이미 A가 존재하는 곳이다. Linear Probing은 그냥 한칸씩 내려가면서 빈 곳을 찾는다. A의 바로 아래 삽입이 된다.




D와 E의 삽입 과정이다. E는 처음에 A의 위치로 매핑이 됐지만 이미 A가 있기 때문에 쭉 내려가면서 3칸을 내려간 곳에 삽입됐다.
검색은 삽입과 동일한 과정을 반복하다가 원하는 key를 찾지 못하고 빈 슬롯을 만나면 검색에 실패한 것으로 간주하고 끝난다.
삭제 연산을 살펴보도록 하자.
삭제시에도 key가 존재하는지 아닌지 확인하는 작업은 필요하다. 그렇게 해서 key를 찾았다고 가정하자.
key가 위치한 곳의 원소를 삭제하고 그 bucket이 비었다고 표시하는 것만으로는 불충분하다.
위에서 검색 연산시에 빈 슬롯이 나올 때까지 Probing을 반복한다고 했다. 아래처럼 C를 삭제하고 비었다고 표시했다고 하자. D를 검색하면 어떻게 될까? 존재하지만 그런 key는 해시 테이블에 없다는 결과를 얻는다.


이를 해결하기 위해 삭제한 bucket을 비었다고 표시하지 말고 어떤 key가 있다가 지워졌다고 표시하는 것이다.
그리고 검색 과정 상에서 이런 표시가 있는 bucket을 만났다면 검색을 계속하도록 하는 것이다. 물론 삽입 시에는 이런 표시가 있는 bucket은 비어있는 것이기 때문에 여기에 삽입을 해도 된다.
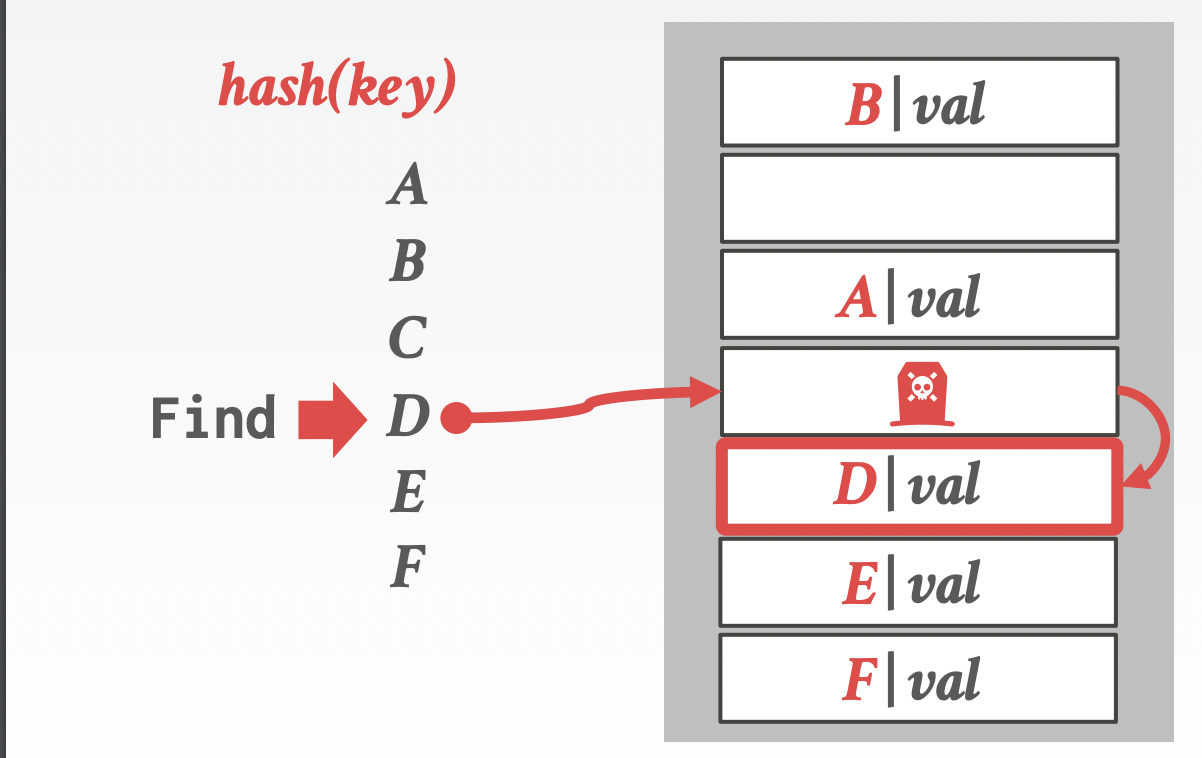
이걸로 충돌을 해결하면서 삽입, 삭제, 검색 연산을 수행할 수 있게 됐다. 당신도 누가 해시 테이블 구현할 줄 아냐고 물어보면 할 줄 알게 됐다는 것이다.
물론 이걸로 끝은 아니다. Linear Probing 방식은 키가 한 곳에 뭉쳐 있게 되는 clustering이라는 부작용을 만들기 쉬운데 이렇게 되면 해시 테이블 상에 원소는 몇 개 없어도 연산 시간이 오래 걸릴 수 있다.
또한 저장된 원소의 수 $n$이 현재 해시 테이블의 크기 $m$에 가까워질수록 꽉 차게 되고 연산 시간이 늘어나게 된다. 이러면 해시 테이블의 크기를 늘리고 새로이 구축해야 한다. 이런 과정을 rehash라고도 한다.
rehash 과정은 $O(n)$이므로 비싼 연산이다. 이 과정을 언제쯤 수행할지 잘 정하는 것도 구현 상의 이슈가 된다. $n=m$일 때 수행한다면 삭제, 삽입이 번갈아 일어나면 쓸데없이 많이 일어난다. 이와 관련해서는 array doubling이라는 것을 이용하면 좋다. 현재 크기의 $\frac{3}{4}$만큼 차면 크기를 두 배로 늘리고 현재 크기의 $\frac{1}{4}$만큼 차면 크기를 반으로 줄이는 방식이다.
쓰면서 생각났는데 지워졌다는 표식을 남기기 때문에 $\frac{1}{4}$만큼 찼다는 걸 판단하는 것도 생각을 잘 해야 할 거 같다. 저 표식이 있는 칸도 채워졌다고 생각하면 절대 안 줄어든다. 그렇다고 저걸 비어있다고 생각하는건 잘못된 거 같다.
Postgresql에서는 Linear Probing을 조금 변형한 Robin Hood Hashing 방식을 simplehash에 사용중인 거 같다. 링크
CMU DB 강의에서는 Robin Hood Hashing과 Cuckoo Hashing을 Linear Probing 외에도 소개해주는데 뒤에 후술할 extendible hashing과 함께 정리할 수 있으면 포스팅을 올릴 거 같다.
Chaining
Open Addressing 방식은 해시 테이블의 크기가 삽입, 삭제 도중에 변하지 않는다. 이에 반해 Chaining과 같이 해시 테이블의 크기를 연산 도중에 변화시키는 방식을 dynamic hashing scheme이라고 한다.
여기서 소개할 Chaining은 굉장히 간단한 방식이다. bucket 별로 key를 하나만 저장하는 것이 아니라 그냥 모든 key를 linked list로 저장해둔다.
서로 다른 key $x, y$의 해시값 $h(x) = h(y) = i$로 같아서 충돌이 일어났다고 해보자.
그러면 $i$라는 bucket은 item을 하나만 가지는게 아니라 이 bucket에 해당하는 linked list를 가지고 있고 이 list에 그냥 key를 추가한다.
좀 더 프로그래밍하는 관점에서 설명하자면 open addressing 방식에서는 hash_table[i]가 item을 가지고 있었다면 chaining은 hash_table[i]는 해시값이 i인 key들이 저장되어 있는 linked list의 포인터를 가지고 있는 것이다.
삽입은 당연히 $O(1)$일 것이다. 이제 검색이 문제인데 검색은 그냥 linked list에서 linear search를 한다.
현재 들어있는 원소의 수가 $n$이고 bucket의 수가 $m$이라면 평균 검색 시간은 $\frac{n}{m}$이 될 것이다. 이 값을 load factor라고 부른다.


위와 같이 테이블의 원소들이 해당 bucket에 해당하는 리스트의 주소를 가리키고 있다. 그리고 linked list로 원소를 추가하며 관리한다.
JAVA의 HashMap은 Chaining 방식으로 구현되어 있다고 한다. 그리고 key들 간의 비교자가 정의되어 있다고 한다면 linked list가 아니라 Balanced Tree를 이용하여 저장한다고 한다.
CMU DB수업에서는 이런 dynamic hashing scheme으로 extendible hashing이나 linear hashing도 소개하지만 그건 추후에 정리하게 되면 포스팅으로 올리도록 하겠다.
그림 출처
https://15445.courses.cs.cmu.edu/fall2020/slides/06-hashtables.pdf
'DB 공부' 카테고리의 다른 글
| Buffer Pool Manager - 2 (0) | 2021.06.25 |
|---|---|
| Buffer Pool Manager - 1 (1) | 2021.06.23 |
| DBMS는 저장소를 어떻게 관리하는가? - 2 (2) | 2021.06.08 |
| DBMS는 저장소를 어떻게 관리하는가? (0) | 2021.06.02 |
| SQL에서 NULL과의 연산 (0) | 2021.05.21 |



